ریاضی به زبان ساده-نوشته های سید علا سبزپوش-www.math2easy.com
آموزش ریاضی - تمرین و نکته هاریاضی به زبان ساده-نوشته های سید علا سبزپوش-www.math2easy.com
آموزش ریاضی - تمرین و نکته هانمایش هندسی مجموعه ها و زیر مجموعه ها
همه ما می دانیم که یک تصویر گاهی می تواند بهتر از یک کتاب ، گویا تر باشد . در ریاضیات تصویر نقش مهمی را ایفا می کند .در نظریه مجموعه ها نیز نمایش هندسی نقش مهمی را ایفا می کند ، یکی از این اشکال ((نمودار ون )) است .
نمودارهای ون، مدلهایی شهودی در نظریه مجموعهها هستند که برای نمایش روابط منطقی و ریاضی بین دو مجموعه به کار میروند. یک نمودار ون همه روابط منطقی بین مجموعهها را نشان میدهد. این نمودارها نخستین بار توسط جان ون، فیلسوف و ریاضیدان انگلیسی در سال 1881 معرفی شدند. در این نمودارها مجموعهها به صورت منحنیهای بسته مشخص میشوند. در شکلها زیر نمودار ون را برای دو مجموعه مشاهده میکنید. به تعداد منحنیهای بستهای که در نمودار ون به کار میرود مرتبه نمودار ون میگوییم

مثالی دیگر :
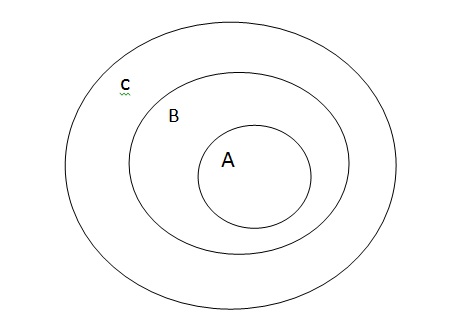
مجموعه اعداد طبیعی N را در نظر میگیریم. همچنین مجموعه A را به شکل روبرو داریم: {2,4,6,...,10,12,...}
مجموعه A زیرمجموعهای از اعداد طبیعی خواهد بود. یعنی هر عضو از A تواماً عضوی از N نیز به حساب میآید. به بیانی دیگر، عضوهای A از بین اعضای N انتخاب شدهاند. پس میتوانیم N را مجموعه مرجعی برای A بدانیم.بنابر این:
هر مجموعه را میتوان مجموعه مرجعی برای تمام زیرمجموعههایش خواند.
به عبارتی دیگر اگر مجموعه ای داشته باشیم که سرگروه و یا تمامی مجموعه ها ، زیر مجموعه آن باشند، آن مجموعه را مجموعه مرجع می نامیم و با نماد M نمایش می دهیم .
متاسفانه مجموعه مرجع در ریاضی نیز جز مفاهیم تعریف نشده است ، و تعریف آن یک تعریف نسبی است مانند مثال بالا .
نکته: مجموعهای بسیار بزرگ و یکتا به نام مجموعه مرجع میتواند وجود وجود داشته باشد که در برگیرنده تمام مجموعه و همه اشیا بدون قید و شرط باشد.مجموعه مرجع جز فرضیات پذیرفته شده است ، همچنین یک مفهوم نسبی است ، یعنی نسبت به فضای مجموعه مقایسه می شود
چند مثال :
اگر A مجموعه دانشجویان دانشکده ریاضی دانشگاه تهران باشد آنگاه M مجموعه مرجع برابر است با تمام دانشجویان دانشگاه تهران
اگر A مجموعه اعداد {1و2و5و5و9و7و1و547} باشد مجموعه مرجع می تواند تمام اعداد طبیعی باشد .
اکنون که با مفهوم جزییت و زیر مجموعه ها و مجموعه مرجع آشنا شدیم ، سوالی مطرح می شود که چند نوع زیر مجموعه وجود دارد . در جواب باید گفت 2 نوع .


ویژگیهای تساوی دو مجموعه :
1-هر مجموعه با خودش مساوی است
2-ترتیب تساوی مجموعه ها مهم نیست یعنی اگر A=B باشد آنگاه B=A نیز می باشد
سوالی دیگر : هر مجموعه می تواند از اعضای خود زیر مجموعه هایی داشته باشد ، سوال این است که هر مجموعه چند زیر مجموعه می تواند داشته باشد ؟
برای جواب به این سوال باید اصل مجموعه توانی را مطرح کنیم ؟
اگر {A={a,b,c یک مجموعه باشد در این صورت زیرمجموعههای A عبارتاند از:
{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c},{ }



سلام...خیلی ممنون و با تشکر....موفق باشید.