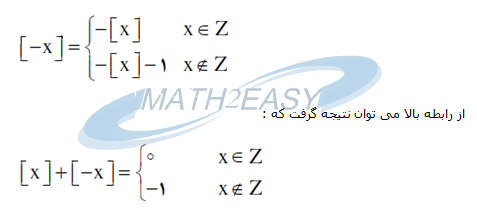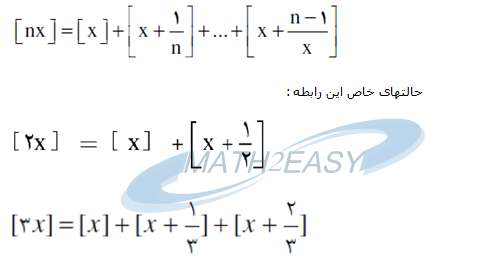ریاضی به زبان ساده-نوشته های سید علا سبزپوش-www.math2easy.com
آموزش ریاضی - تمرین و نکته هاریاضی به زبان ساده-نوشته های سید علا سبزپوش-www.math2easy.com
آموزش ریاضی - تمرین و نکته هاخواص جزء صحیح که باید بدانید
در این پست که به در خواست و بنابر سوال کاربران است ، تصمیم دارم برخی خواص جز صحیح را بیان کنم و در همان حال راهی برای اثبات آنها نیز ارایه دهم علاوه بر این کاربردهای آن را نیز با هم مرور خواهیم کرد .پس اکنون تک تک خصوصیات جز صحیح را با هم مرور می کنیم .
۳- به ازای هر x متعلق به اعداد حقیقی R و k عدد صحیح یعنی متعلق به مجموعه Z داریم که:
[x]+k =[x+k]
4- به ازای هر x متعلق به اعداد حقیقی R داریم که :
۵- اما حالا می رسیم به یک رابطه بسیار مهم که به آن رابطه آیزنشتاین (Eisenstein) می گویند به ازای هر x متعلق به اعداد حقیقی R و n متعلق به اعداد صحیح Z داریم:
چگونه ریاضی را آسان بفهمیم؟
اگر به دنبال مطالب آموزشی در زمینه فهم راحتتر و بهتر ریاضی هستید
اگر میخواهید ریاضی را آسان بیاموزید
حتما از سایت ما که شامل مطالب آموزشی ریاضی است بازدید کنید
مجانب افقی
مجانب افقی چیست ؟
چگونه محاسبه می شود؟
آیا یک تابع می تواند بیش از یک مجانب افقی داشته باشد ؟
آیا مجانب افقی می تواند با منحنی تابع تقاطع داشته باشد ؟
برای دیدن جوابهای خود به لینک زیر بروید
حد توابع مثلثاتی در بی نهایت
حد توابع مثلثاتی در بی نهایت
شاید برای شما سوال باشد که چگونه می توان حد توابع مثلثاتی را در بی نهایت بدست آورد ، یا اصلا حد این توابع در بی نهایت وجود دارد ، خوب قبل از هر چیز شما باید به دامنه تابع خود دقت کنید ، به تعبیری دیگر ما هر گاه بخواهیم دامنه تابعی را در نقطه ای محاسبه کنیم بهتر است ابتدا ببینیم که آیا این نقطه در دامنه تابع تعریف شده یا نه ؟ اگر این نقطه در دامنه تابع ما تعریف نشده باشد پس این تابع در آن نقطه هم حد ندارد ، بنابراین با همان دلیل می گوییم ، تابع سینوس و کسینوس در بی نهایت حد ندارد .
برای دیدن ادامه مطلب در سایت ما