تعریف تابع

فرض کنیم x   زمانی باشدکه از لحظه پرتاب یک سفینه فضایی می گذرد ، و y   مکانی باشد که سفینه در این زمان در آنجا قرار دارد ، واضح است که x   ( زمان ) در هر لحظه مقدار منحصر به فردی دارد . اما موقعیت مکانی سفینه y   می تواند تکراری باشد . یعنی اگر در زمان 2 بعد از ظهر سفینه در مکان 700 کیلومتری باشد ، پس از طی زمانی مثلا در ساعت 8  شب می تواند دوباره به همان مکان بازگردد . حال اگر ما زمان و موقعیت زمانی سفینه را بصورت زوج مرتب (x,y)   نمایش دهیم . خواهیم داشت .که  x  همواره مقدار منحصر به فردی است .اما y  می تواند تکراری باشد و جالب اینجاست که اگر x  تکراری باشد پس حتما y  هم باید تکراری باشد .

اکنون با این مقدمه تعریف تابع از چند لحاظ مطرح می کنیم .

1-تعریف تابع از لحاظ زوج مرتب  

یک تابع مجموعه ای از زوج مرتب است ، که در آن هیچ دو زوج مرتبی دارای مولفه اول یکسان نباشند در غیر این صورت اگر مولفه های اول یکسان باشند آنگاه مولفه های دوم هم حتما باید مساوی باشند .

مثال 1 : آیا { (3,4),(7,6),(1,2)}  این رابطه یک تابع است ؟

جواب :بله یک تابع است . چون در تمام زوجهای مرتب بالا عناصر اول منحصر به فرد هستند و یکسان نیستند

مثال 2:آیا {(1,2),(1,2),(3,4),(5,9)} این رابطه یک تابع است ؟

جواب : بله تابع است . اگر چه دارای زوج مرتب با عناصر یکسان و تکراری است ، اما عناصر دوم این زوجهای مرتب نیز مساوی هستند .

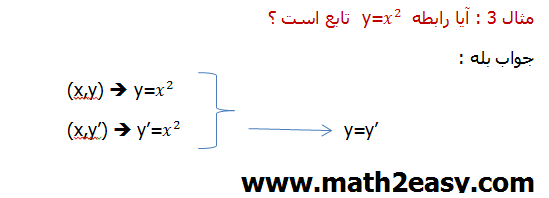
مثال 3 : آیا { (1,2),(1,4),(3,2)} این رابطه یک تابع است ؟

جواب : خیر تابع نیست . چون دو زوج مرتب دارد که مولفه های اول آنها یکسان است اما مولفه های دوم آنها  یکسان نیست .

2-تعریف تابع بصورت نمودار ون

هر گاه در نموداری ، A  مجموعه  اول و B  مجموعه  دوم باشد و پیکانهایی از مجموعه A  به مجموعه B  داشته باشیم . این نمودار نمایش دهنده تابع است ، هر گاه از هر عنصر مجموعه A  فقط یک پیکان به سمت مجموعه B  داشته باشیم .

نکته 1: در این نمودار از برخی عناصر مجموعه A  ممکن است هیچ پیکانی خارج نشود ، در اینصورت اگر شرط بالا صادق باشد ، نمودار تابع است .

مثال 1 : نمودار زیر یک تابع است ، چرا که از هر عنصر مجموعه A  فقط یک پیکان خارج شده است .

 

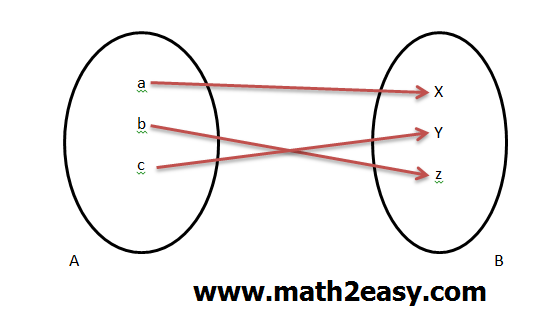
مثال 2 : نمودار زیر تابع است . زیرا از هر عنصر مجموعه  A  فقط یک پیکان خارج شده است و همچنین طبق نکته گفته شده ( نکته با رنگ سبز) از یکی از عناصر هیچ پیکانی خارج نشده است .

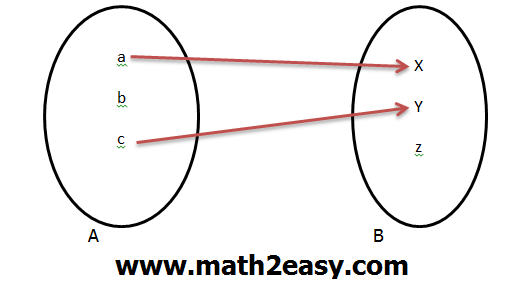
مثال 3 : نمودار زیر تابع نیست . چون از یکی ، از عناصر مجموعه  اول دو پیکان خارج شده است .

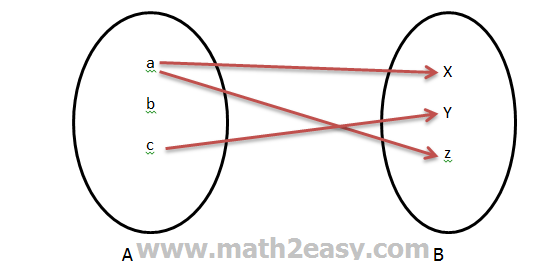
3- تعریف تابع از دیدگاه ریاضی با ضابطه

اگر فرض کنیم A  و B  دو مجموعه  باشند آنگاه f  را تابعی از مجموعه A  به مجموعه B  می گویند .هر گاه به ازای هر عضو x  از مجموعه A  عضو منحصر به فردی مانند  y  از مجموعه B  نسبت داده شود . و چنانچه عضو y  منحصر به فرد نباشد ( تکراری باشد ) پس عنصر x  هم باید تکراری یا یکسان باشد و تابع را به صورت                        y=f(x)    نمایش می دهیم .

نکته 2 :با بیان ریاضی چگونه می توان فهمید که یک ضابطه f  از A  به B  تابع است ؟

جواب آن به این شکل است . که اگر  f   یک ضابطه از A  به B  است . آنگاه خواهیم داشت :

(x,y)   زوج مرتب متعلق به ضابطه f

(x,y’)  زوج مرتب دیگری که باز هم متعلق به ضابطه f است .

اکنون از دو زوج مرتب بالا ، چون دو هر دو زوج مرتب مولفه های اول یکسان هستند پس مولفه های دوم نیز باید یکسان باشند یعنی    y=y’

مثال 1 : آیا  y=2x+1   تابع است ؟

جواب : اگر (x,y)  زوج مرتب باشد آنگاه ضابطه ما همان  y=2x+1

         اگر (x,y’)  زوج مرتب دیگری باشد آنگاه ضابطه ما  y’=2x+1 خواهد بود

حالا چون در دو زوج مرتب بالا مولفه های اول یکسان هستند باید ثابت کنیم مولفه های دوم نیز یکسان هستند

 پس داریم :

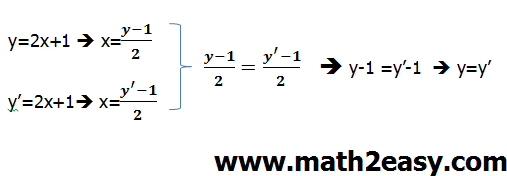
پس ضابطه بالا تابع است .

اگر  x  در هر دو زوج مرتب یکسان باشد از رابطه بالا داریم که

 

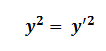
اما  y , y’  مساوی نیستند پس ضابطه بالا تابع نیست