عملیات مقدماتی در مجموعه ها

با نگاهی به بخشهای قبلی دانستیم که هر مجموعه اعضایی دارد و زیر مجموعه ، یک مجموعه مرجع است ، هر مجموعه متممی دارد و غیره

اکنون این سوال مطرح می شود که آیا می تواند بین 2 یا بیشتر از 2 مجموعه ، ارتباطی ایجاد کرد ، و یا ترکیباتی با هم ایجاد کرد مثلا آیا می توان مجموعه ها را با هم ادغام کرد و یا از هم کم کرد و یا نقاط مشترک بین مجموعه ها را پیدا کرد . برای جواب به این سوال باید چند عمل مقدماتی در مجموعه ها را شرح دهیم

اعمال مقدماتی در مجموعه ها عبارتند از : 1-اجتماع 2-اشتراک 3-تفریق یا تفاضل

1-اجتماع مجموعه ها :

اجتماع دو مجموعه A , B را بصورت A نمایش می دهند و بصورت زیر تعریف می کنیم

اگر عضوهای دو مجموعه $A$ و $B$ را در مجموعهٔ دیگری بریزیم . مجموعه جدیدی بدست می آید که هر عضو آن به مجموعه A یا مجموعه B یا هم به A و هم به B تعلق دارد .

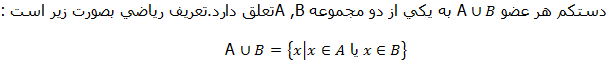
یعنی x یا متعلق به مجموعه A است یا متعلق به مجموعه B است یا متعلق به هر دو مجموعه است .

در زیر نمودار ون اجتماع چند مجموعه را نمایش می دهیم

الف-اجتماع دو مجموعه متداخل

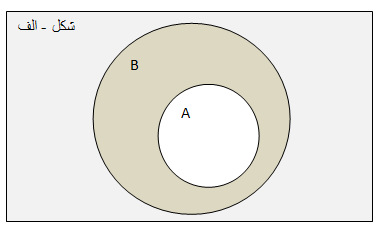
مثلا مجموعه A زیر مجموعه مجموعه B است همانطور که از شکل واضح است

نتیجه برابر مجموعه B خواهد بود . یعنی اجتماع این دو مجموعه برابر مجموعه بزرگتر B است .

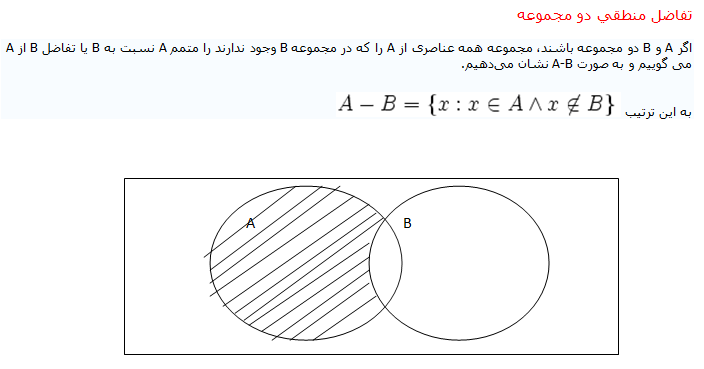
ب- اجتماع دو مجموعه متقاطع : به دو مجموعه متقاطع می گوییم هر گاه دارای عناصر مشترک باشند مانند نمودار ون زیر اجتماع دو مجموعه متقاطع برابر ، برابر تمام اعضای A و تمام اعضای B به اضافه عناصر مشترک هر دو مجموعه است.